회귀(Regression) 모델의 성능을 평가할 때는 예측값과 실제값 사이의 차이를 수치화하여 얼마나 정확하게 예측했는지를 확인합니다.
회귀(Regression)모델은 연속적인 값을 예측하는 데 사용됩니다. 이때 예측의 정확도를 수치적으로 판단해야 하며, 이를 위해 여러 지표를 사용합니다. 대표적인 성능 지표 MAE, MSE, RMSE, MAPE, MPE, R² 에 대해서 정리 합니다.
회기 모델 성능 지표: MAE, MSE, RMSE, MAPE, MPE, R²
목차1. MAE(Mean Absolute Error): 평균 절대 오차
2. MSE(Mean Squared Error): 평균 제곱 오차
3. RMSE(Root Mean Squared Error): 평균 제곱근 오차
4. MAPE(Mean Absolute Percentage Error):평균 절대 백분율 오차
1. MAE(Mean Absolute Error): 평균 절대 오차
예측값과 실제값 사이의 절댓값 차이의 평균입니다.
모든 오차를 동등하게 취급하므로 이상치에 덜 민감합니다.

◆ 절대값을 쓰는 이유
- 오차는 양수(과대 예측)도 있고 음수(과소 예측)도 있습니다.
- 단순히 평균을 내면 +와 –가 서로 상쇄되어 실제로는 큰 오차가 있음에도 "0에 가까운 좋은 성능"처럼 보일 수 있기 때문입니다.
- 그래서 절댓값을 써서 오차의 크기만 반영합니다.
◆ 해석 예시
- MAE = 3.2 → 예측값은 실제값에서 평균 ±3.2만큼 오차를 가집니다.
- MAE = 0 → 예측이 완벽히 정확
- MAE = 5 → 예측이 평균적으로 5 단위만큼 벗어남
- 실제값: 100, 예측값: 97 → 오차 = 3 → MAE에 그대로 반영
◆ 특징
- 단위는 그대로 유지되므로 해석이 쉽습니다 (가격, 시간, 수량 등)
- 큰 오차에 덜 민감하여 전체적인 평균 오류를 파악할 때 적합
2. MSE(Mean Squared Error): 평균 제곱 오차
MSE는 오차의 크기를 제곱해서 평균낸 값으로, 큰 오차가 발생하면 그 영향력이 크게 반영됩니다.
정밀한 예측이 필요한 상황이나, 이상치를 강조하고 싶은 경우에 효과적인 성능 지표입니다.

◆ 제곱하는 이유
- 큰 오차를 강조하기 위함.
- 단순 평균(MAE)에서는 오차 10과 오차 1이 거의 비슷하게 취급되지만, MSE는 오차 10이 100점의 영향력을 줍니다

◆ 해석 예시
- MSE = 25 → 오차의 평균 크기가 약 5 (5² = 25) 정도로 볼 수 있음
- 실제: 100, 예측: 90 → 오차 = 10 → 102=10010^2 = 100 → MSE 크게 증가
- 단위는 제곱 단위이기 때문에, 해석은 RMSE가 더 직관적입니다.
◆ 특징
- 의료 수치 예측이나 금융 리스크 분석처럼 작은 실수 하나가 큰 문제로 이어질 수 있는 분야에서는 MSE가 유용하게 사용됩니다.
- MSE는 수학적으로 미분이 가능하다는 점에서, 머신러닝 알고리즘에서 최적화 과정에 유리하다는 장점도 가지고 있습니다.
- MSE는 정밀한 예측을 요구하는 상황에서 강력한 도구가 될 수 있지만, 해석의 직관성 부족과 이상치에 대한 민감도는 고려해야 할 요소입니다.
3. RMSE(Root Mean Squared Error): 평균 제곱근 오차
MSE는 MSE(평균 제곱 오차)의 제곱근을 씌운 값입니다.
RMSE(Root Mean Squared Error)는 예측값이 실제값과 평균적으로 얼마나 차이 나는지를 직관적으로 표현할 수 있는 회귀 성능 지표입니다.
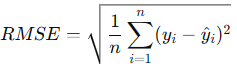
즉, 오차를 제곱하여 평균을 낸 다음, 다시 그 값에 제곱근을 적용한 것입니다.
이렇게 하면 MSE보다 해석이 더 직관적이 되고, 단위도 실제값과 동일해집니다.
◆ 해석 예시
- MSE = (25 + 16 + 25 + 4 + 25) / 5 = 19
- RMSE = √19 ≈ 4.36
- 평균적으로 ±4.36분 정도 오차가 발생한다고 이해할 수 있습니다.
- RMSE = 10 → 예측값이 실제값과 평균적으로 약 ±10 단위 정도 차이
- 단위는 실제값과 같아서 (예: 원, 분, 개수 등) 실무에 사용하기 쉽고 직관적입니다.
◆ 특징
- RMSE는 MSE의 장점인 큰 오차에 대한 민감함을 유지하면서도, 단위 문제를 해결해 실무에 더 적합합니다.
- MSE의 특성을 그대로 가져오기 때문에, 이상치(Outlier)가 존재할 경우 결과가 왜곡될 수 있는 단점도 있습니다.
- 큰 오차 하나가 전체 RMSE 값을 높여버릴 수 있기 때문에, 데이터 전처리나 이상치 처리 없이 사용하면 왜곡된 판단을 할 위험도 있습니다.
- 배달 시간, 응답 속도, 추천 시스템 정확도처럼 사용자가 실제로 느끼는 오차 크기가 중요한 경우, RMSE는 단순 수치가 아닌 “예측이 평균적으로 이만큼 틀렸다”는 식으로 바로 설명이 가능합니다.
4. MAPE(Mean Absolute Percentage Error): 평균 절대 백분율 오차
MAPE는 예측 오차를 "백분율(%)"로 환산하여 평균낸 값입니다.
오차를 원 단위나 시간 단위가 아닌 “퍼센트(%)”로 표현하기 때문에,
데이터의 크기나 단위에 상관없이 서로 다른 모델이나 데이터셋을 비교하기에 적합한 지표입니다.

*“예측값이 실제값과 몇 % 정도 차이나는가”를 평균적으로 나타냅니다.
◆ 해석 예시
- MAPE = 8% 라면, 모델의 예측값은 실제값과 평균적으로 약 8% 차이가 난다는 의미입니다.
- 단위는 없기 때문에, 원, 분, 개수 등 단위와 무관하게 평가 가능합니다.
◆ 사용 예
- 단위가 서로 다른 데이터 비교가 필요할 때
- 예: 가격(원), 수요(개), 수익률(%) 등 다양한 단위를 가진 데이터
- 경영지표, 성과비율, 수익률 등 퍼센트 기반 분석이 필요할 때
- 모델 성능을 일반 사용자나 비전문가에게 쉽게 설명해야 할 때
- 예: "우리의 매출 예측 시스템은 평균적으로 실제 매출에서 5% 정도의 오차가 있어요."
◆ 유의사항
- 실제값이 0이 되거나 0에 가까우면,
- → 오차율이 무한대(inf) 또는 비정상적으로 커지는 오류 발생
- → 데이터에서 실제값이 0에 가까운 항목을 제외하거나, SMAPE, MAE 등 다른 지표와 병행 사용
- MAPE는 예측값이 낮을 때(과소 예측), 오차 비율이 더 커집니다.

- 이는 리스크 보수적인 모델이 더 불리하게 평가받을 수도 있음을 의미합니다.
5. MPE(Mean Percentage Error): 평균 백분율 오차
MPE는 예측값이 실제값보다 평균적으로 얼마나 높은지(과대 예측), 낮은지(과소 예측)를 백분율로 계산해 보여주는 지표입니다.

예측 오차의 방향(방향성 있는 편향)을 확인할 수 있다는 것이 가장 큰 특징입니다.
일반적인 오차 지표(MAE, MAPE 등)는 오차의 크기만 측정합니다.
→ 하지만 예측이 항상 과소되었는지, 항상 과대되었는지는 알 수 없습니다.
MPE는 오차의 부호(+)와 (−)를 유지하여,
→ 예측값이 평균적으로 실제보다 높은지 또는 낮은지를 보여줍니다.
◆ 해석 예시
- MPE = +1.43% : 예측값이 실제보다 평균적으로 1.43% 더 높게 나오는 경향이 있다
즉, 과대 예측(bias) 존재 - MPE = -4%
→ 평균적으로 예측값이 실제보다 4% 더 낮게 나옴 (과소 예측)
◆ 사용 예
- 예측 시스템이 편향되어 있는지(biased) 확인하고 싶을 때
- 예: 수요 예측 시스템이 항상 수요보다 적게 예측하는가?
- 모델이 과대 또는 과소 예측하는 경향을 보정하려 할 때
- 예: 광고 예산을 계획할 때 항상 초과 예상하는 문제를 조정
- MAPE = 6%, MPE = -2%
→ 예측은 평균적으로 6% 정도 틀렸고, 그 방향은 실제보다 2% 작게 나오는 경향
◆ 특징
- 오차 방향(양/음)을 반영하여 과소/과대 예측 편향 분석 가능
- MAPE처럼 % 단위로 단위 없이 해석 가능
- 실제값이 0에 가까우면 MAPE와 마찬가지로 MPE도 불안정
→ 0 나눗셈 문제 또는 과도한 값 발생 - 과소/과대가 번갈아 나타날 경우 평균 MPE가 0 근처가 되어,
→ 실제 모델 성능이 좋지 않은데도 정확한 것처럼 보일 수 있음
6. R²(R-squared) : 결정 계수
R²는 회귀 모델이 전체 데이터의 변동(분산)을 얼마나 잘 설명하고 있는지를 나타내는 지표입니다.
쉽게 말해, "모델이 실제 데이터의 패턴을 얼마나 잘 따라가고 있는가?"를 평가합니다.
하지만 변수가 많을수록 과도하게 높아질 수 있고, 과적합 모델도 높은 R²를 가질 수 있으므로,
단독 지표보다는 RMSE, MAE, Adjusted R² 등과 함께 사용해야 보다 신뢰성 있는 평가가 가능합니다.
값의 범위: 0 ~ 1 사이
- R² = 1 → 완벽하게 설명 (모델 예측이 실제와 정확히 일치)
- R² = 0 → 아무런 설명도 못함 (무작위 예측 수준)

모델이 예측한 값들이 실제값의 평균보다 오차가 더 작을수록, 즉 모델이 평균보다 더 잘 맞췄을수록 R²는 1에 가까워집니다.
◆ 해석 예시
예: R² = 0.92
- 모델이 전체 데이터의 분산(변동성) 중 92%를 설명하고 있다는 뜻
- 즉, 모델이 대부분의 데이터 패턴을 잘 포착하고 있음
예: R² = 0
- 모델의 예측값이 실제값 평균과 차이가 없음
- 즉, 무작위 예측과 동일한 수준의 설명력
예: R² = 1
- 모델이 모든 데이터를 완벽히 예측
- 예측값 = 실제값 (오차 없음)
"이 모델은 매출 데이터를 약 85% 수준으로 설명할 수 있어요."
7. 성능 지표 요약 비교
| 지표 | 실무 활용 | 특징 설명 |
| MAE (Mean Absolute Error) |
가격 예측, 수요 예측, 교통 시간 예측 | 예상치 민감도: 낮음 오차의 절댓값 평균. 큰 오차에 덜 민감하고 직관적임. 실무에 많이 사용됨. 해석: MAE = 3.2 → “예측값이 실제값과 평균적으로 ±3.2만큼 차이 남 예시: 실제값 100, 예측값 97 → 오차 3 → MAE에 그대로 반영 |
| MSE (Mean Squared Error) |
의료 예측, 금융 위험도 평가 | 예상치 민감도: 높음 오차를 제곱해서 평균하므로 큰 오차에 매우 민감함. 이상치가 중요하거나 큰 오차를 절대 피해야 하는 분야에서 적합. 해석: MSE = 25 → 오차가 평균적으로 5 정도 클 수 있음 (5² = 25) 예시: 오차 10 → 10² = 100 → 큰 오차 하나가 전체 MSE 상승시킴 |
| RMSE (Root Mean Squared Error) |
시스템 응답시간 예측, 고객 대기시간 예측 | 예상치 민감도: 높음 MSE에 제곱근 적용. 해석이 MAE보다 더 자연스럽고 직관적. 해석: RMSE = 4 → 평균 ±4 정도의 오차 발생 해석: 실제값 100, 예측값 96 → 오차 4 → 직관적 이해 가능 |
| MAPE (Mean Absolute Percentage Error) |
판매량, 이익률, 매출 예측 등 비율 기반 데이터 | 예상치 민감도: 중간 예측 오차를 비율(%)로 나타내므로 단위가 없어 다양한 항목 간 비교 가능. 하지만 실제값이 0에 가까우면 값이 폭등해 주의 필요. 해석: MAPE = 8% → “예측값이 실제값 대비 평균 8% 차이 남 예시: 실제 200, 예측 180 → 10% 오차 → MAPE에 반영 |
| MPE (Mean Percentage Error) |
과대·과소 예측의 경향 파악, 영업전략 보완 | 예상치 민감도: 중간 예측이 평균적으로 실제보다 높은지(과대), 낮은지(과소) 파악 가능. 방향성 파악에 특화된 지표이나, 양수/음수가 섞이면 상쇄될 수 있음. 해석: MPE = -4% → “예측값이 실제보다 평균 4% 더 높게 나옴 (과대 예측)” 예시: 실제 100, 예측 104 → +4% 과대 예측 |
| R² (결정계수) |
모델 전반 성능 평가, 여러 모델 비교 | 예상치 민감도: 간접적 오차 크기 자체는 알려주지 않지만,모델이 실제 데이터를 얼마나 잘 설명하는지 %로 나타냄. 1에 가까울수록 우수한 모델. 단독 사용보다는 MAE, RMSE와 함께 사용 권장. 해석: R² = 0.92 → “데이터 분산의 92%를 모델이 설명함” 예시: 0.0 = 무작위 예측 수준, 1.0 = 완벽한 예측 |
- MAE = 3.2 → 예측이 평균적으로 실제보다 약 ±3.2만큼 차이 남.
- MAPE = 8% → 예측이 평균적으로 실제값의 8% 정도 차이 남.
- MPE = -4% → 예측값이 평균적으로 실제보다 4% 높게 나옴 (과대 예측).
- R² = 0.92 → 모델이 92%의 데이터 분산을 설명, 모델이 사용한 변수들로 잘 설명하고 있음.
- RMSE > MAE 차이가 크면? → "이상치(큰 오차)가 많다"는 신호일 수 있음.
8. 모델 성능 평가 예시 : 집값 예측 모델
부동산 데이터를 기반으로 서울시 아파트의 실거래가를 예측하는 회귀 모델을 만들었다고 가정해봅시다.
◆ 평가 지표 결과
| 지표 | 값 | 해석 |
| MAE | 3,200만 원 | 예측이 실제 가격에서 평균 ±3,200만 원 정도 오차가 발생 |
| RMSE | 4,800만 원 | 큰 오차에 더 민감하게 측정했을 때도 약 ±4,800만 원 수준의 오차 발생 |
| MAPE | 7.6% | 예측이 실제 거래가보다 평균적으로 7.6% 차이 |
| MPE | +1.8% | 예측값이 평균적으로 실제값보다 1.8% 더 높게 나오는 경향 (과대 예측) |
| R² | 0.91 | 전체 집값 데이터의 91% 변동성을 모델이 설명하고 있음 → 높은 설명력 |
◆ MAE = 3,200만 원
- “예측값은 평균적으로 실제 집값과 3,200만 원 정도 차이가 나며, 단위 그대로 해석이 가능합니다.”
- 실무에서 금액 기준으로 예산 오차 범위를 평가할 때 유용
◆ RMSE = 4,800만 원
- “큰 오차가 존재하는 경우가 있고, 이를 반영하면 평균적으로 약 4,800만 원의 오차가 발생합니다.”
- 큰 손해나 이익을 우려해야 하는 투자자/개발사에 중요
◆ MAPE = 7.6%
- “예측값이 실제 거래가보다 평균 7.6% 오차가 있습니다.”
- 퍼센트 기반이라 동일 모델로 다른 지역 예측할 때도 비교가 용이
◆ MPE = +1.8%
- “예측 모델이 평균적으로 실제 집값보다 1.8% 정도 더 높게 예측하고 있습니다.”
- 가격을 과대 평가하는 경향이 있어, 모델을 보수적으로 조정할 필요 있음
◆ R² = 0.91
- “이 모델은 집값 변동성의 91%를 설명할 수 있을 만큼 높은 설명력을 보입니다.”
- 즉, 모델은 시장 트렌드나 지역 특성 반영에 효과적
◆ 종합 평가 예시
이 회귀 모델은 서울 아파트 실거래가 예측에서 전체 데이터의 91%를 설명할 만큼 높은 설명력을 보이며, 평균적으로 약 3,200만 원(7.6%)의 오차를 가집니다.
다만, 예측값이 실제보다 평균 1.8% 정도 높게 나오는 경향이 있어, 보수적인 평가가 필요한 실거래 활용 상황에서는 보정 계수 적용이 필요합니다.
전반적으로 정확도와 설명력이 우수하며, 투자 및 실무 분석에 충분히 활용 가능한 모델입니다.
관련 글 링크
https://vitalflux.com/mse-vs-rmse-vs-mae-vs-mape-vs-r-squared-when-to-use/#google_vignette
MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to Use?
Learn about when to use which evaluation metrics of regression models - MSE, RMSE, MAE, MAPE, R-Squared. Learn with Python & R Code Examples
vitalflux.com
'5. IT기술노트 > 인공지능' 카테고리의 다른 글
| 딥러닝 모델 양자화(Quantization)란? : 경량화 (0) | 2025.05.19 |
|---|---|
| 객체 탐지 모델 성능 지표:IoU,Precision,Recall,AP,mAP,FPS (0) | 2025.04.23 |
| 분류 모델 성능 지표: Confusion Matrix (0) | 2025.04.23 |
| 이미지 분석 기술: Classification, Object Detection, Segmentation (0) | 2025.04.22 |
| 전이 학습(Transfer Learning):Fine-tuning (0) | 2025.04.16 |